The development of out-of-core techniques suitable for processing highly irregular, unstructured data, such as are generated by cosmological N-body simulations, is crucial to manipulating a dataset of sufficient size. We have recently obtained extremely promising results applying parallel, out-of-core techniques to the irregular and dynamic treecode methods that are used within the N-body integrator itself [9]. Essentially, the problem reduces to one of guaranteeing spatial and temporal locality so that access to secondary storage is necessary only rarely, and once loaded from secondary storage, a given datum is likely to be re-used many times in primary storage before being flushed. The solution is exactly the same one that has been employed to good effect to achieve load balance and tolerate latency in parallel implementations of treecodes -- organize and divide the data along a space-filling curve that approximately preserves spatial locality even if the underlying data is highly clustered and irregular. The crucial observation is that by placing the pages dynamically on disk in an order determined by a continuous space-filling curve, e.g., a Peano-Hilbert curve, (see Figure 7) and ordering our access to data along the same curve, we preserve the spatial and temporal locality in the algorithm. Since the space-filling curve is continuous, objects that are near in space, and hence likely to be linked together by the algorithms, are also near in primary or secondary storage. By visiting objects in order along the space-filling curve, objects that were recently brought into primary storage, either because they were directly addressed, or because they are on the same page as a recently addressed object, are likely to be reused. Since the parallel implementation of the spatial halo finder uses the same data and control structures as the N-body code to tolerate irregularity and achieve parallelism, it can be adapted to use out-of-core storage in the same way that has worked for the N-body code itself.
Figure:
A path through the positions of 10000 highly clustered particles in
two dimensions is shown in (a). The path is obtained by locating
each particle along a space-filling Peano-Hilbert curve. Levels 4,
6 and 8 of an adaptive quad-tree are shown in (b), (c), and (d).
The squares represent ``cells'' in an adaptive quad-tree that is
used to compute densities and locate neighbors in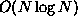 
time.
The whole tree is obtained by ``stacking'' these levels, along with
those not shown.
Again, the path connecting the cells is derived from a Peano-Hilbert
curve. In this case, the curve indicates the order in which data
are stored in both primary and secondary memory. Each level of the
tree is stored separately, so that data within the same level is always
contiguous.
When particles are
visited in the order implied by (a), they cause pages to be moved
from secondary storage which hold data that is contiguous along the
curves represented in (b), (c), (d). The orderings guarantee that
the data is reused many times before being discarded, allowing the
algorithm to tolerate the modest bandwidth and extreme latencies
characteristic of out-of-core calculation. (Two dimensions are used
purely for ease of graphical representation. The implementation is
fully three-dimensional.)