Data Structures

  The fundamental data structure in a tree code is, of course, the tree, and the fundamental operation is a tree traversal. A two-dimensional version of the basic data structure is shown in Figure 1. In three dimensions, space is divided into cubical sib_groups, each of which may contain some terminal bodies as well as up eight moment structures - i.e., a data structure that contains a pointer to a daughter sib_group, as well as numerical quantities like mass, center-of-mass, and higher moments of the distribution within the region. In an in-core version of the algorithm, the arrows in Figure 1 would correspond to normal ``C'' pointers, but in the out-or-core implementation, they are implemented as oocptrs.

 

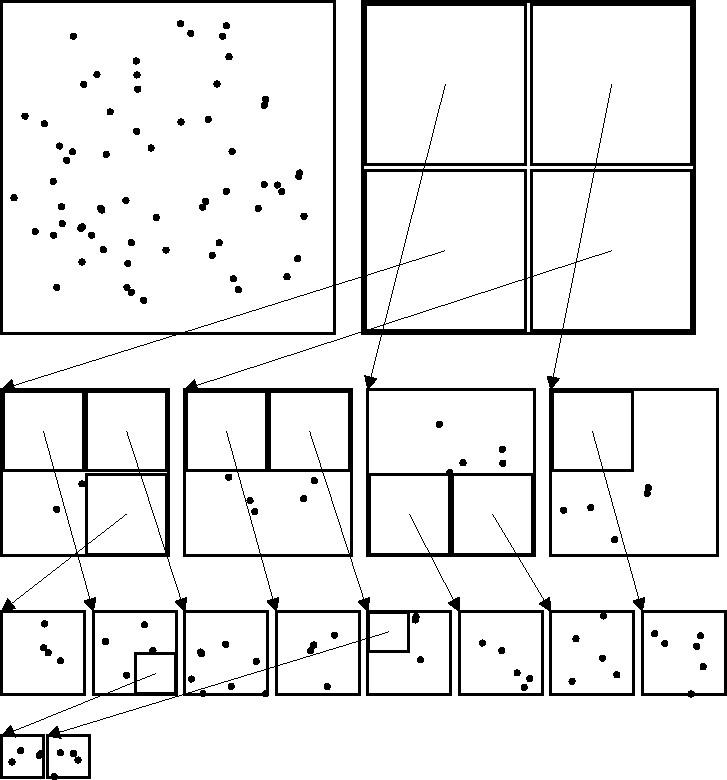
Figure 1:   The elements of the tree data structure are shown for a two-dimensional quad-tree with 64 bodies, and a terminal threshold m=3. The upper left square shows just the bodies without any imposed tree structure. The other squares are sib_groups, which contain both moment data (represented as an inset square) and individual bodies, stored together in memory. In addition to cumulative information about the contents the cell, the moment structure also contains a pointer to a daughter sib_group where more detailed information may be found. These are shown as arrows in the figure and are implemented as oocptrs in the parallel out-of-core code.

The depth of the tree is irregular and adapts to local variations in the density of bodies. A moment is only created when the number of bodies in its region of space exceeds some threshold, m. If there are insufficient bodies in the region, then the bodies become terminal members of the surrounding sib_group.

The basic traversal algorithm is shown schematically in Figure 2. When a moment is 'visited', a numerical criterion is applied to determine whether to use the moment data in the force calculation or to traverse the deeper, finer-grained levels of the tree.

 
Figure 2:   Pseudocode representation of the basic tree-traversal algorithm.

Traverse is called repeatedly by a larger loop that orders the force evaluations and allows the programmer to use VisitAndTest routines that consider groups of particles together, possibly implementing a ``local expansion'', or deferring force evaluation to a vectorizable loop that is executed once per particle. Notice that Traverse visits every member of a sib_group whenever it visits one of them. Therefore, by grouping all the moments in a sib_group together, we enhance fine-grain data locality, which in-turn improves our cache-hit rate and overall performance. This is helpful to an in-core implementation, but it is particularly important to an out-of-core implementation because it allows us to amortize the cost of the OOCRef and OOCUnRef over the fairly substantial calculations implied by VisitAndTest and VisitTerminals.

Data locality is further enhanced by the order in which forces are evaluated on bodies. We choose the order in which we compute forces to maximize re-use of sib_groups in the tree. If the cache is large enough to hold all the sib_groups that contribute to the force on a body, and we then compute the force on a nearby body, we will find almost all the information necessary for the second body already in cache. We have found that by ordering particles along a self-similar, space-filling curve, like the Peano-Hilbert curve shown in Figure 3, we achieve excellent spatial locality and cache hit rates [6].

 

Figure 3:   A Peano-Hilbert curve induced ordering of 10000 bodies. Bodies are assigned the same color in groups of 50 at a time, indicating how they would be grouped on pages in out-of-core storage.

Again, strategies that favor cache reuse in an in-core implementation are crucial to an out-of-core implementation. Even a very modest working-set of a few hundred pages is large enough to store the interaction set of a typical body. So the device of ordering evaluations so that sequential bodies substantially share interaction sets leads to very high reuse rates for the working set and correspondingly low swap rates in the out-of-core case.

The placement of sib_groups within pages is not an issue for an in-core implementation because there is no reason not to use malloc to obtain space whenever a new sib_group is created. Since the sib_group itself is comparable in size to a typical cache-line, there is not much benefit in carefully arranging them with respect to one another. Many sib_groups, however, fit on a single out-of-core page, and we must ensure re-use not only of the sib_group that has been OOCRefed, but also the others that happen to reside on the same page. Thus, pages should contain sib_groups that are likely to be used together. We achieve this by storing sib_groups at the same level in the tree together, and ordering them along the same space-filling curve used to order force evaluations. Thus, when a new page is swapped in to satisfy an OOCRef to a particular sib_group, the other sib_groups on the page are nearby in space and they will probably be accessed shortly, at which time they will already be in memory, and subsequent OOCRefs will impose minimal overhead.

Figure 3 illustrates the spatial clustering achieved by ordering bodies along the Peano-Hilbert curve. Inspection of Figure 3 (in color) reveals that in the vicinity of any given point in space, there are no more than four colors represented (eight in three dimensions). The same spatial locality properties will hold for sib_groups at every level of the tree. This suggests that we will need a working set sufficiently large to hold, in the worst-case, eight pages at each level of the tree. Even for systems with many millions of particles, the tree rarely exceeds a depth of 20. so we expect that only 160 or so pages devoted to our tree data structure should be an adequate working set. Results in Section 7 confirm this hypothesis.